Introduction
A page dedicated to the atom and its constituents. At first the text may be incoherent but the plan is to gradually accumulate data and rework it in good time.
A page dedicated to the atom and its constituents. At first the text may be incoherent but the plan is to gradually accumulate data and rework it in good time.
This chapter on orbitals uses a selection from Wikipedia articles.
Electrons exist in atomic orbitals, which are a set of quantum states of the negatively charged electrons trapped in the electrical field generated by the positively charged nucleus.
An atomic orbital is a mathematical function that describes the wave-like behavior of either one electron or a pair of electrons in an atom.
This function can be used to calculate the probability of finding any electron of an atom in any specific region around the atom's nucleus. These functions may serve as three-dimensional graphs of an electron's likely location. The term may thus refer directly to the physical region defined by the function where the electron is likely to be.
Atomic orbitals exactly describe the shape of this region only when a single electron is present in an atom. When more electrons are added to a single atom, the additional electrons tend to more evenly fill in a volume of space around the nucleus so that the resulting collection (sometimes termed the atom's electron cloud) tends toward a generally spherical zone of probability describing where the atom's electrons will be found.
Following image shows the basic shapes of the orbitals
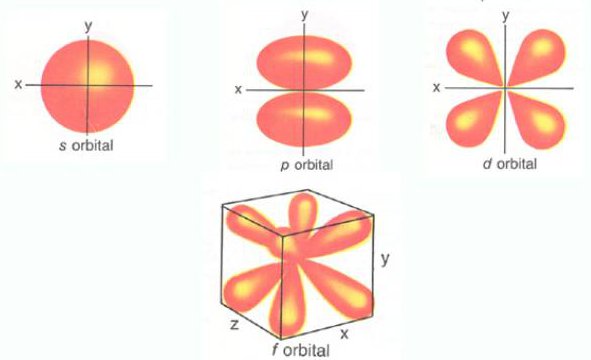
The simple names s orbital, p orbital, d orbital and f orbital refer to orbitals with angular momentum quantum number l = 0, 1, 2 and 3 respectively.
[names of orbital shapes] are derived from the characteristics of their spectroscopic lines: sharp, principal, diffuse, and fundamental, the rest being named in alphabetical order (omitting j). The atomic spectral lines correspond to transitions (quantum leaps) between quantum states of an atom.
This section is inspired by a series of videos by Sal Khan. His website Khan Academy contains talks on many educational topics.
Determining energy shells for atoms usually involves quite a complicated scheme using special diagrams. But recently my attention was drawn to a different method, one that involves using the periodic table. This system is much easier to absorb and has the added bonus that it makes you more familiar with the periodic table.
It is an interesting fact that the elements in the periodic table are organized in such a way that each column holds elements that share some fundamental characteristics, largely due to their valency electrons - which will come into the discussion later on.
Here's a skectch of the periodic table, with just a few elements that will be used in the examples. Note that I moved the He element, which is usually located to the far right of the same row, next to the H element. This just makes the explanation a little easier.
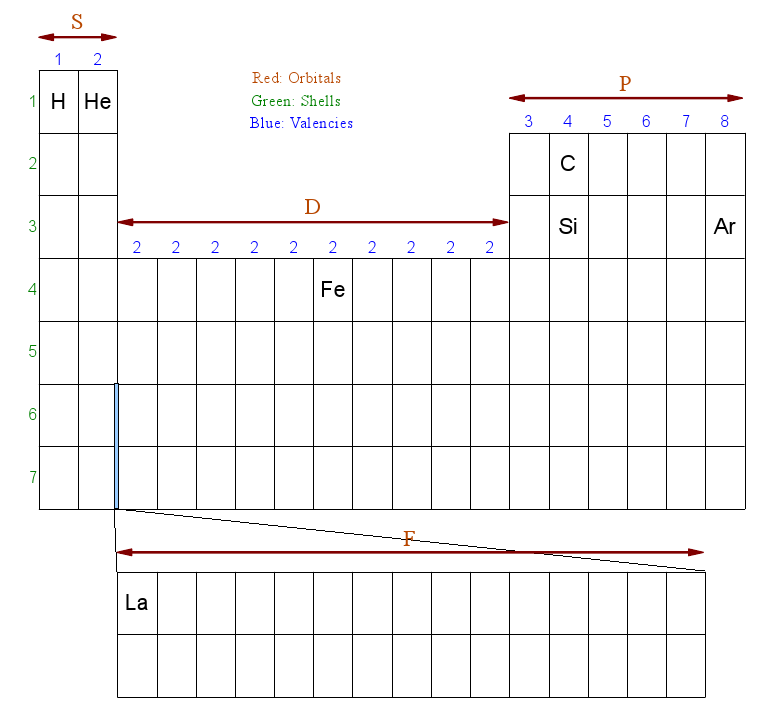
The red letters S, D, P, and F denote the shape or subshell of the orbital.
The green numbers correspond to the electron energy levels, the further away the electrons are from the nucleus the higher this energy tends to be, while its Coulomb force or Charge will become weaker. It is these high energy electrons that will be involved in the chemical reactions.
Orbitals are given names of the form:
nOy
where n is the energy level, O is a letter denoting the shape or subshell of the orbital, and y is the number of electrons in that orbital.
The periodic table is organized in such a way that it becomes easy to calculate the electron configuration for each element.
For example, Hydrogen's shell configuration is 1S1, meaning its lone electron resides in the 1st energy level and forms a probability cloud in the shape of an S-orbital (which is a sphere). The last '1' just means it has 1 electron.
Helium (He) has a configuration of 1S2. Like Hydrogen, it has the same energy level and the same orbital shape, but it has 2 electrons instead of one. This is how we derive this information from the periodic table sketch above:
The '1' points to the fact that the element resides in the first row (period). 'S' because it resides in the red 'S' zone, and '2' because it is the second element in that S zone row.
If you're confused, all will become clear in the examples. Let's take Carbon (C), which has 6 electrons. We need to walk through the periodic table (from left to right - like a book) and fill all the shells up to the element Carbon:
That's it. The result is 1S2 - 2S2 - 2P2. Add up the number of electrons to confirm that C has 6 electrons: 2 + 2 + 2 = 6
Take Silicon, which has 14 electrons (assuming no isotopes) and apply the same reasoning:
The result is 1S2 - 2S2 - 2P6 - 3S2 - 3P2. Add up the number of electrons to confirm that Si has 14 electrons: 2 + 2 + 6 + 2 + 2 = 14
When we get to the elements that reside in the D and F Shells, there is something we have to take into consideration. As we get further away from the nucleus, there's much more space available. As a result the electrons in these higher shells tend to fall into these gaps (hence the smart-alec title of this page). This leads to the following rules:
Again, this will become clear in our following example, Fe which has 26 electrons:
Note how we reduced 4D6 to 3D6. Note the results in order:
1S2 - 2S2 - 2P6 - 3S2 - 3P6 -
3D6 - 4S2
Note that even though there are 6 electrons in the D shell, the higher energy shell only has 2. This is the reason that Fe has a valency of 2 and not 6. This is also the reason that metals in this group tend to have lots of free electrons. These are the electrons in the D shell that can freely move around while not affecting its valency electrons, which determine its chemical properties.
Another thing to note is that we tend to repeat things. The first lines in all these
examples above are the same. Actually, we can say that Fe has all the electron
configuration properties up to Argon with some extra bits, which we can notate in the
following way:
[Ar] - 3D6 - 4S2
The last example concerns the element La, which has 57 electrons:
Result: 1S2 - 2S2 - 2P6 - 3S2 - 3P6 -
3D10 - 4S2 - 4P6 - 4D10 - 4F1 -
5S2 - 5P6 - 6S2.
Giving a total of 2 + 2 + 6 + 2 + 6 + 10 + 2 + 6 + 10 + 1 + 2 + 6 + 2 = 57
There's a great program, Orbital Viewer that lets you view these orbitals and alter its parameters. It requires you to convert the used notation using quantum numbers, which is another topic I would like to add eventually. Its pdf file contains a lot of interesting information.
Electrons are more accurately described as standing waves surrounding the nucleus.
It was not until 1926 that the solution of the Schrödinger equation for electron-waves in atoms provided the functions for the modern orbitals.
For example, the orbital 1s2 has two electrons and is the lowest energy level (n = 1) and has an angular quantum number of l = 0. In X-ray notation, the principal quantum number is given a letter associated with it. For n = 1, 2, 3, 4, 5, ..., the letters associated with those numbers are K, L, M, N, O, ... respectively.
An atomic orbital is uniquely identified by the values of the three quantum numbers, and each set of the three quantum numbers corresponds to exactly one orbital, but the quantum numbers only occur in certain combinations of values.
The principal quantum number, n, describes the energy of the electron and is always a positive integer. In fact, it can be any positive integer, but for reasons discussed below, large numbers are seldom encountered. Each atom has, in general, many orbitals associated with each value of n; these orbitals together are sometimes called electron shells.
The azimuthal quantum number, ℓ, describes the orbital angular momentum of each electron and is a non-negative integer. Within a shell where n is some integer n0, ℓ ranges across all (integer) values satisfying the relation 0 ≤ ℓ ≤ n0 - 1. For instance, the n=1 shell has only orbitals with ℓ=0, and the n=2 shell has only orbitals with ℓ=0, and ℓ=1. The set of orbitals associated with a particular value of ℓ are sometimes collectively called a subshell.
The magnetic quantum number, mℓ, describes the magnetic moment of an electron in an arbitrary direction, and is also always an integer. Within a subshell where ℓ is some integer ℓ0, mℓ ranges thus: -ℓ0 ≤ mℓ ≤ ℓ0.
In Quantum Mechanics, the above phenomenon is explained using Quantum Numbers.
Heres's how to relate the above Orbital model to its quantum numbers:
Subshells are usually identified by their n and ℓ values. n is represented by its numerical value, but ℓ is represented by a letter as follows: 0 is represented by 's', 1 by 'p', 2 by 'd', 3 by 'f', and 4 by 'g'. For instance, one may speak of the subshell with n = 2 and ℓ = 0 as a '2s subshell'.
Free Software that enables you to manipulate and view atoms in 3D, including stereoscopic effects. The pdf document is also very informative.
Atomic OrbitalWikipedia page about atomic orbits. A little scattered, but great GIF animations in the chapter Understanding why atomic orbitals take these shapes shows the orbits represented as standing waves on circular drums.